
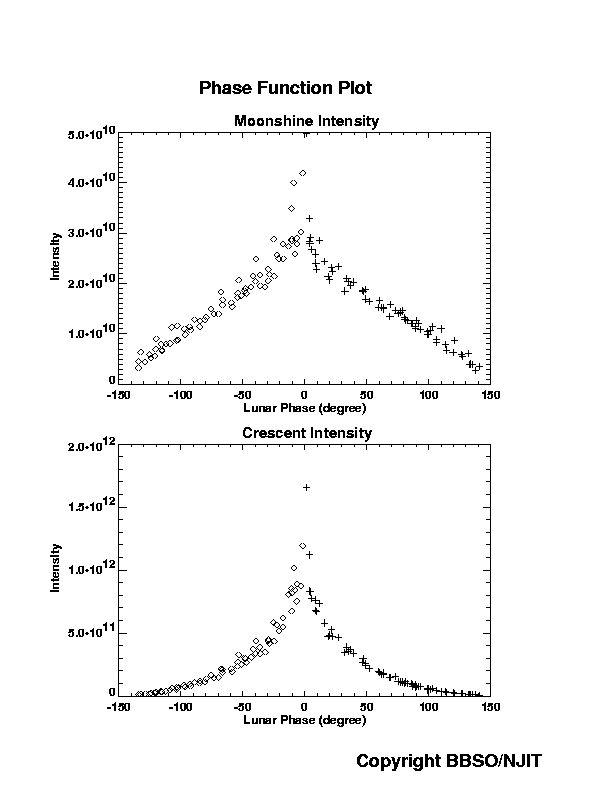
| Lunar Phase Function |
| Beer's law fitting | Beer's law fitting |
 |
 |
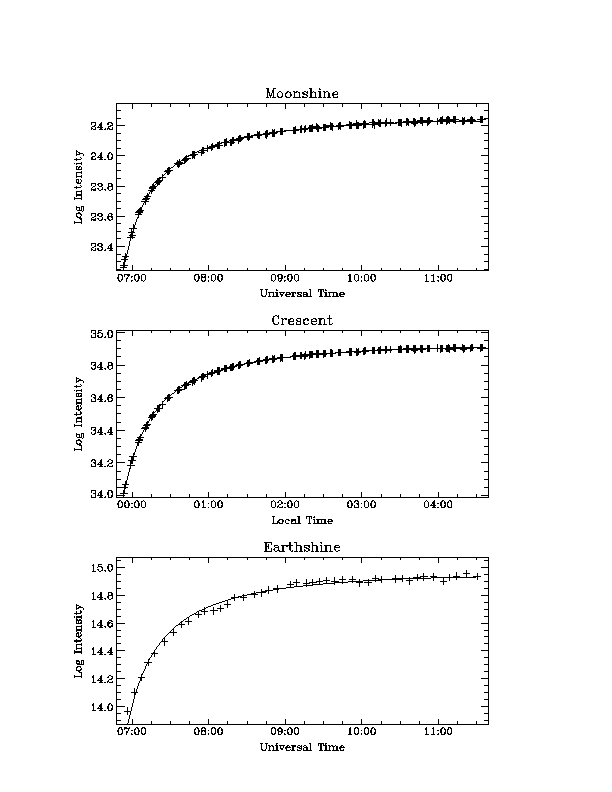
| Fig.1a Intensity against time | Fig.1b Intensity against airmass |
| (click here for PostScript file) | (click here for PostScript file) |
 (click here for PostScript file)
(click here for PostScript file)
 (click here for PostScript file)
(click here for PostScript file)