Abstract. The Earth's climate depends on the net sunlight deposited on the globe, which is critically sensitive to the Earth's albedo. A global and absolutely calibrated albedo can be determined by measuring the amount of sunlight reflected from the Earth and, in turn, back to the Earth from the dark portion of the face of the Moon (the `earthshine' or `ashen light'). Such data provide a critical complement to satellite data. We propose to advance our investigation into the systematic determination of the Earth's albedo through the measurement of earthshine with two parallel efforts.
First, we will continue to observe from Big Bear Solar Observatory (BBSO) using our earthshine `coronagraph', and analyze the resulting data. BBSO is a site characterized by cloudless skies and excellent seeing. The products of our proposed efforts will be a four-year collection of albedo data, containing the 18 months already in hand, as well as an analysis of the relation of the albedo to satellite derived cloud-cover data. We propose to extend the observations to measurements of the infrared component of the earthshine, which will represent a significant expansion of the wavelength band in which the Earth's albedo has been determined. The albedo data will also enable us to quantitatively assess the global effects of transient phenomena such as volcanic eruptions and El Nino Southern Oscillations (ENSOs), in addition to providing details on seasonal and secular variations. Finally, the data in hand cover the solar activity minimum which is just ending, and the three years of new data will cover the rising phase of the new cycle, allowing us to determine the level of solar cycle dependence. These products are all significant for climate models.
Second, we will extend our modeling of earthshine by using more recent scene models (giving surface character and fractional cloud cover) developed for the Earth Radiation Budget Experiment (ERBE) satellite observations and corresponding general circulation model (GCM) derived cloud and snow/ice covers to simulate both earthshine and the Earth's Bond albedo (ratio of total light reflected in all directions to the total incident light). The integrated albedo obtained from our observations will provide a unique check on how well the models represent the surface and cloud components of the albedo.
We have not received prior NASA support for the earthshine project. The interdisciplinary earthshine program was established under funding to Koonin from the Western Regional Center of the National Institute for Global Environmental Change; in Section II (Proposed Research), we discuss relevant progress made with that support.
The energetics of our climate system are dominated by the radiative transfer of energy from the Sun to the Earth and from the Earth to space. The Earth's energy balance is determined in large part by its albedo - the fraction of the incident sunlight that is directly reflected back into space without altering the internal energy budget of the atmosphere and oceans. The Earth's surface, aerosols in the atmosphere, and clouds all reflect some of the incoming solar short-wavelength radiation, preventing that energy from warming the planet. Short-wavelength radiation, usually defined as having wavelengths between 0.15 and 4.0 µm, includes about 99% of the Sun's radiation; of this energy, 46% is infrared (>0.74 µm), 9% is ultraviolet (<0.4 µm) and the remaining 45% is visible, with wavelengths between 0.4 and 0.74 µm. A significant portion of the solar energy is absorbed by the Earth, where it drives terrestrial phenomena before being radiated back into space. This latter long-wavelength radiation peaks at about 15 µm (a black-body temperature of TE=255 K).
The power going into the Earth's climate system is
Pin=C \pi RE2 (1-A),
where C is the solar constant, RE is the Earth's radius and A is the short-wavelength Bond albedo determined to be 0.30 by ERBE satellite measurements, Gibson, et al. (1990). Similarly, the long-wavelength power that the Earth radiates into space is
Pout=4 \pi RE2 \sigma \epsilon TE4,
where \sigma is the Stefan-Boltzmann constant and \epsilon is the emissivity of the atmosphere (at about 5.5 km high, where the long-wavelength radiation is emitted).
If the planet is in radiative equilibrium, Pin=Pout,
and we have
TE4=C (4 \sigma \epsilon)-1(1-A).
This means that the Bond albedo directly controls the Earth's temperature.
The fundamental importance of albedo in determining the Earth's radiation budget, and the variety of mechanisms affecting the albedo - which has synoptic, seasonal, and annual variability, as well as longer-term solar cycle variations - point to the importance of accurate albedo measurements over a long period of time. The global albedo, averaged over a variety of time scales, is therefore a crucial climate indicator, but its determination remains a challenging task. We propose to continue a modern program based on an old, but largely forgotten, means for obtaining the global average albedo. The method involves observing the dark part of the lunar disk to measure `earthshine' - the sunlight reflected by the Earth to the Moon and then back to Earth.
This technique has a number of advantages over measurements that might be made, for instance, with a satellite. Because the earthshine is directly compared with the sunlit lunar crescent, we have absolute calibration, whereas satellite observations are difficult to calibrate and tend to degrade, exacerbating calibration problems. In addition, because the Moon is so distant, we obtain a `global' integration of the albedo, unlike satellite observations which yield only a patch albedo. Because our instrument is on the ground, a large, calibrated CCD may be used. And, of course, the enterprise is far, far cheaper! We view our observations as being complementary to those from satellites. In addition, we intend these observations to be long term, and they therefore can link data from, say, one satellite to its successors.
The most important historical program of earthshine measurements was carried out by Danjon (1928, 1954) from a number of sites in France, but primarily from Provence. He used a `cat's-eye' photometer to produce a double image of the Moon, allowing the visual comparison of the intensities of two well-defined patches of the lunar surface - one in sunlight and the other in the earthshine - at various lunar phases. Using the `cat's-eye' mechanism, he stopped down the light from the sunlit portion to match the brightness of the ashen portion. This differential measurement removed many of the uncertainties associated with varying atmospheric absorption and the solar constant, allowing Danjon to achieve an estimated uncertainty of roughly 5%. With a different instrument, our observations are made from Big Bear, California.
After an extensive site survey, Big Bear Lake was selected for Caltech's daytime observatory. The site was chosen because of its more than 300 cloudless days per year, and the particular stability of the air above the lake. A recent site survey of the major solar observatories in the world has shown that Big Bear has, by far, the least turbulent air. Turbulence is the enemy of all ground-based astronomy. Big Bear has proven also to be a superb site for nighttime observations of the earthshine. In Big Bear, not only do we have clear skies, but the earthshine instrumentation is in place and our staff is experienced in making these observations. Our observing experience has taught us we can measure the earthshine intensity to at least a few percent - after careful observation and data reduction. We can do much better than in Danjon's time, in part, through use of CCD camera systems. As well, we can make observations closer to full Moon, where scattered moonlight becomes a problem which we overcome by use of a `coronagraph'.
On July 1, 1997, the management of Big Bear Solar Observatory was transferred from Caltech to NJIT. Nonetheless, Caltech remains in close partnership. The partnership is reflected in this proposal.
From 1926 to 1930, Danjon made 207 measurements of earthshine. Dubois (1947) continued the program through 1960 from the observatory at Bordeaux using a Danjon-type photometer; he also added various color filters to obtain the spectral variation of earthshine.
Danjon's and Dubois' results show a number of interesting features. The daily mean values of the observations vary more widely than would be expected on the basis of the variation of measurements on a single night. This can be plausibly attributed to daily changes in cloud cover, but extensive cloud-cover data were not available at the time of the observations. Today, earthshine observations can be fruitfully compared with cloud-cover observations made by operational meteorological satellites.
Svensmark and Friis-Christensen (1997) have studied satellite cloud cover data and measured a 3-4% greater cloud cover at solar activity minimum. They argue that this implies solar cycle climatological variations more than an order of magnitude larger than those implied by observed solar irradiance variations over the cycle. They further argue that the source of the excess cloud cover is the relatively greater cosmic radiation at activity minimum which arises from the Sun's magnetic field being weaker at activity minimum and, thereby, being less effective in shielding the Earth from cosmic radiation. According to their argument, the relatively greater cosmic radiation creates relatively more ions which have a correspondingly greater cloud-seeding effect. The details of their interpretation of the cloud data may or may not be correct, but the apparent terrestrial magnification of solar effects emphasizes the importance of looking for long term trends in the albedo as an indicator of global climate change.
Danjon (1928) also examined his observations to determine whether there was a long-term trend in albedo, but found none above their noise level. Our noise level is considerably lower than his. Dubois' observations for some 20 years ending in 1960 showed considerable annual variability, which he speculated was due to solar activity. His published monthly variations from 1940-1944 also show a strong correlation with the 1941-42 ENSO event.
In the past 37 years, there have been some observations of earthshine by Huffman et al. (1989) and one-time observations by Franklin (1967) and Kennedy (1969).
Danjon used his observations to estimate the mean global albedo. Since the observations are only at visible wavelengths, they must be corrected for the balance of the short-wavelength radiation, most of which is in the near IR. Estimates of this correction were made by Fritz (1949), after taking into account the decrease of the Earth's albedo with increasing wavelength (our `blue planet'). This difference points up the importance of extending the observations into the near IR, as we propose. Fritz also attempted to correct for the geographical bias in Danjon's observations. The western hemisphere, which was most frequently observed by Danjon, has a greater fraction of land than does the globe as a whole, implying that Danjon's value would be high because the sea is dark compared to land. Combining the decreases from the absence of the IR and geographical bias, Fritz found that Danjon's visual albedo of 0.40 corresponds to a Bond albedo (considering all the wavelengths and directions) of 0.36.
Flatte et al. (1991) noted that a correction must be made for the `opposition effect' present in lunar reflectance properties. Observations of the Moon show that the Moon's reflectivity has a strong angular dependence. This `lunar phase function' can rise by as much as a factor of two in going from 5° to 0° (exact backscattering). This enhancement was once thought to be due to the porous nature of the lunar surface (Hapke 1971) and was unknown in Danjon's time. More modern work has shown it to be caused by coherent backscatter in the lunar soil. The smallest lunar phase angle measured by Danjon was only 11°. The extent of the small-angle rise varies over different regions of the lunar surface, but can easily be the 20% required to reduce Fritz's value of 0.36 to the aforementioned 0.30 (Buratti et al. (1997)).
In a modern context, earthshine measurements have a number of attractive features. Albedo is a basic parameter of the climate system, and ground-based measurements that integrate on a global scale are rare. Earthshine observations would complement more detailed satellite studies and could, at a minimum, serve as a cross-check on scene and temporal modeling; cloud observations and scene models could then be used to predict the time variation of earthshine, and these predictions could be compared with observations.
We also propose to combine Danjon's observations (and subsequent ones based on his technique) with ours because the combination could provide a unique window on changes in the Earth's climate in this century. We are not sanguine about this because of the relatively larger intrumental noise in the old set-up, and the geographical differences; but the comparison is important and we will do it very carefully.
Modern photometry can achieve far more accurate results than the state-of-the-art in the 1920s, and hundreds of observations have replaced Danjon's 50 points per year. Our CCD and IR array detectors have sufficient resolution and dynamic range to observe both the sunlit and earthshine portions of the Moon in the same image (although a dark filter is usually interposed on the bright crescent), so the entire disk is measured at once. Large format imaging arrays to extend observations to the near infrared are becoming available, and we have two such cameras in Big Bear. For the future, but not as part of this proposal, an extension of our initial single-site program to three observing sites, appropriately spaced around the globe, would suffice for continuous coverage during the majority of each month. By that time, we should have automated the observing process to minimize manpower requirements at the remote sites.
We propose to continue a successful program. The proposed research largely depends on the observing, analyzing and modeling techniques that we have already developed, so we describe them here. We emphasize that our observational technique is quite different from that of Danjon.
Over a period of approximately eighteen months (December 1993 to March 1995), we have:
The normal BBSO earthshine data consist of four pairs of `white light (i.e. no colored filter) images of the Moon and four pairs with colored filters, IR (>700 nm), R (600-700 nm), G (500-600 nm), B (400-500 nm). Each pair consists of a short exposure of the bright crescent and a longer exposure with the bright crescent of the Moon covered by a neutral filter to reduce its brightness to roughly that of the dark earthshine side. These images are taken at intervals of approximately 20-30 minutes between sunset and moonset (evening runs) or between moonrise and sunrise (morning runs). (A gap of 20-30 minutes is short enough to allow us to obtain the time-of-day changes in the Earthshine by the rotation of the Earth while limiting our data sets to a manageable size.) At the end of each run, the dark current of the CCD camera is determined for each exposure time used that night. We plan to introduce a flat-fielding program to further improve the accuracy.
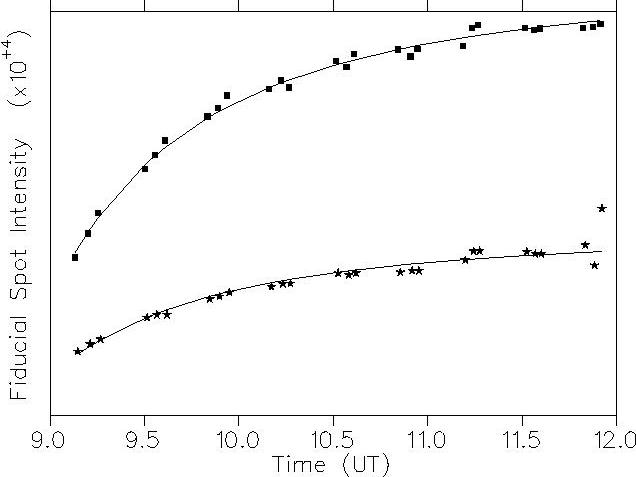
An accurate knowledge of the reflectivity of each observed portion of the lunar surface as a function of phase angle is necessary to compare earthshine observations at different phases, as well as to derive absolute values for the Earth's albedo. To obtain optimal accuracy in the determination of albedo, there are subtle corrections that must be applied, like corrections for the effects of libration (a three dimensional rotation to bring all lunar features to their standard selenographic positions). We have tried in past years to normalize the CCD intensities by comparing CCD images with well-chosen stars at the same elevation as the Moon. However, we found that the accuracy of these measurements was only 2 or 3 percent, and that we could do better by taking a series of measurements of the Moon at different zenith angles, and extrapolating to zero air mass (as though the Earth had no atmosphere). This can be seen in the adjoining (Fig. 1) Beer's Law plot; the stars are the Earthshine and the boxes are from the bright part of the Moon, with an excellent fit to Beer's Law (the solid lines). In addition to this extrapolation, the accuracy of the fit is an externally-imposed selection criterion for the usability of the data, automatically eliminating nights with highly variable local weather conditions.

Fig. 1. Time series of white-light sunshine (boxes) and Earthshine (stars). The Earthshine intensities are in fact 5000 times lower, and have been scaled to fit on the plot. The solid lines are fits to Beer's Law, I0 = I exp (-\alpha z), where \alpha is the fit parameter for the atmosphere and z is the airmass, a function only of the coaltitude angle. These data are from the night of June 2nd, 1994.
While the observations determining the lunar phase function at phase angles larger than about 6° can be pursued at any time, a lunar eclipse offers a unique opportunity to quantify the opposition peak in the lunar reflectance necessary to normalize the phase function. Serendipity granted us a total lunar eclipse in Big Bear on November 28th, 1993, and it was a cloud-free night.
The lunar eclipse data allow us to determine, in slices, the lunar phase function to within approximately 0.8° of full Moon (the limit imposed on ground-based measurements by the Earth's shadow). During the entire night of the eclipse (about 12 hours), we took white-light images of the Moon at approximately half-hour intervals, giving a phase angle resolution of some 15'. Approximately every two hours, a full set of images through the three colored filters was taken as well. A total of almost 300 images was collected.
The data reduction is based on the Danjon technique described in the Introduction: the intensities of well-defined patches on the sunlit and earthshine sides of the lunar disk are compared. This ratio, together with the angular dependence of the reflectivity of the bright-side patch (determined in a separate measurement) and the Earth-Moon distance, allows the instantaneous reflectivity of the Earth to be determined.
For each night of observation, the image files are reduced to a series of bright- and dark-side intensities by a relatively simple yet delicate process. The algorithm used (detailed below) is currently implemented in a portable 6,000 line IDL program.
The data reduction currently involves the following sequence of steps, carried out independently on each image:
The analysis code is run in a fully automatic mode; however, it produces large quantities of data that must be reviewed, both automatically and manually, for consistency. (Unfortunately, the extreme variation in the quality of the images, due to uncontrollable effects such as changes in cloud cover during the course of a night's observation, requires that the analysis be at least partly manual.)
The automatic portion of the analysis of a single night's data can vary from between 1 hour to over 10 hours, depending on the number of images taken. The manual review of the output typically takes less than 30 minutes.
We now show two figures which summarize our previous results and also demonstrate what we expect to obtain in our new observations.
Figure 2 shows a dark-side image of the Moon from February 5th, 1995.

Fig. 2. Image of the Moon. The crescent part (containing Mare Crisium) is blocked by a filter, allowing an exposure of the dark side, in which Grimaldi is clearly visible. These two features are our primary reference points for analysis.
Figure 3 shows two important measurements: Figure 3a shows 23 data points for the fiducial spot intensity on the crescent side, including one point near 0° phase angle. This latter point is critical, allowing us to normalize the lunar phase function to 1. As shown here, the phase function for the fiducial spot we are using is linear over 100°, rising sharply over the last 40° because of the opposition effect. The phase function shape is only critical for data analysis between 140° and 80°, because for phase angles outside that range, we cannot get an accurate measurement of the Earthshine.
Figure 3b shows our measurement of the integrated crescent intensity (solid boxes) against Rougier's measurement from 1933 (solid line). While the actual shape is different, we emphasize that the disagreement is likely due to the increased accuracy of our observations: the improved field depth at the edge of the lit crescent adds significantly to the intensities at mid-range phase angles, as seen here.

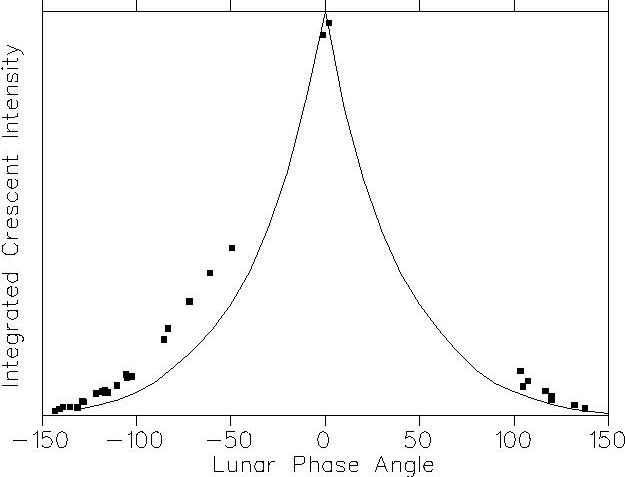
Fig. 3. (a) Fiducial spot Moonshine intensities for evening observations; we have relatively few data points for morning observations. The point at -3° emphasizes that there is an opposition effect. (b) Measured crescent intensity vs. Rougier's data.
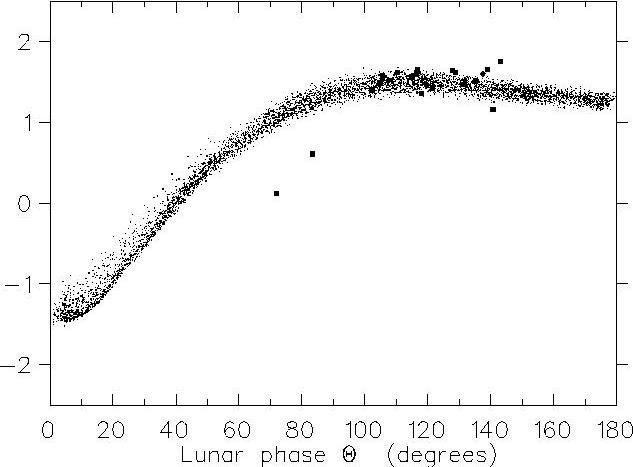
Fig. 4. Modeling vs. data [A*], where [A*] is the logarithm of the effective albedo (Koonin et al., 1998).
Figure 4 shows the results of the analysis of the data from 1995, plotted against the modeling results from Koonin et al., 1998. The agreement is quite clear in the range from 100° to 145° lunar phase angle; this range is particularly important, because it dominates the integral that determines the global (or Bond) albedo, that is, the albedo averaged over all angles. Dubois' value for the variance of the Earthshine is approximately twice the width of that found in the simulation, leading us to suspect that the simulation's cloud-cover model is inadequate.
The two points at 70° and 85° lunar phase are not statistically significant; it is not clear whether the difference between our measurements and the simulation is due to experimental error - in particular, the scattering from the bright side is significantly higher at low phase angles - or is again due to inadequate model parameters. Additional observations are needed to clarify this issue.
We have completed the first modern modeling of earthshine. These calculations use ERBE scene models and GCM-derived cloud and snow/ice covers to simulate both earthshine and the Earth's Bond albedo. The simulated seasonal average albedo is now 0.299. This is shown in Fig. 4 in terms of the effective albedo defined in Koonin, et al. (1998). In the simulations, we find an excellent correlation between the earthshine and albedo; we find (theoretically) that a 1% precision in a measurement of the earthshine intensity leads to an absolute precision in the albedo of 0.002; we are working towards this level of precision in our experimental measurements. A paper describing this work will be submitted simultaneously with our `results' publication. We plan to extend this modeling activity to use satellite-derived cloud and snow/ice cover.
A long-term earthshine monitoring program will make unique contributions to studies of global change. Annual variation in the albedo are of great interest, as is its correlation with global mean surface temperature. The albedo at various phases of the Moon (the phase function) may be more sensitive to global warming than is its integral (the phase integral) which is directly related to the Bond albedo because of the averaging implicit in integration. Isolated events such as any future Pinatubo-like eruption could also be properly monitored, and a truer appreciation of their effects on climate obtained.
We propose to obtain further data on the Earth's albedo, and then to compare it to cloud-cover data and models, determine the dependence on seasonal and secular parameters, and extend our observations to the near infrared.
Our bare-bones objectives are to:
Our current exposures are limited by the guiding of the telescope in declination. The BBSO drive on which the lunar telescope piggybacks is designed for solar tracking rates, having an offset-pointing closed-loop servo system with a Sun sensor. None of these is correct for lunar tracking, and the normal photoelectric guider cannot see the Moon. The right ascension tracking motor has now been replaced with a stepper motor running at 60 rpm for solar rates and 57.97 rpm for lunar rates. The hardware for declination tracking has been purchased and tested, and it will be installed when new funding starts.
We plan to replace the BBSO 1024x1024 12-bit OSL camera for visible light earthshine data acquisition. Beyond the issue of the difficulty and danger of interchanging cameras, we have had to push a camera appropriate for studies of the Sun near the edge of its usefulness. For the earthshine observations, we require a 512x512, 16-bit camera with low noise and dark current - a cooled camera to get as long an exposure time as possible. We will use our 320x240 cooled InGaAs camera for the near IR (0.9-1.7 µm). A Pentium Pro-2 PC will be used to collect and preprocess the images. The data will then be transferred to the UltraSPARC II at BBSO for analysis.
To accumulate significant data, one must continue to observe night after night, so that seasonal, annual and other patterns can be determined. In spite of the somewhat tedious nature of this work, observers seem to be especially drawn to making the measurements, and we anticipate no trouble in recruiting one. The sequence of observations has been described above; we anticipate a more intensive observing schedule as the aforementioned improvements are made to the telescope optics and lunar tracking.
Measurements at various lunar phases are central to our program. The improvements to the instrument and observing procedures during the coming months will allow an expansion of the observing program to phases closer to full Moon. We also will compare existing data and make coordinated observations with Donald Huffman in Arizona, who is making visual observations with a Danjon-type instrument. This will help make the best possible cross-comparison of our data with that of Danjon and Dubois.
As our observing schedule intensifies, we will simultaneously refine our analysis procedures to take advantage of the greater accuracy and density of the observations. In particular, we hope to better quantify the daily and hourly variation of the intensity and color of the earthshine. We also hope to reduce the dependency of the data analysis on manual inspection, thus reducing the time needed for data reduction.
With our sensitivity, greater by far than Danjon's optical observations, we will investigate the possibility of a correlation of the earthshine to the solar cycle. Danjon mentioned the possibility of such a correlation, and Lockwood et al. (1991) found an unexplained anticorrelation between variations in Neptune's brightness and the solar cycle.
Perhaps of more importance to the observational program, we plan in the coming year to use cloud cover from meteorological satellites to calculate, in almost real time, what the earthshine should be. We have made preliminary inquiries into obtaining such data over the Internet; the largest problem so far has been in processing data from disparate sources which is in different formats.
In addition to the Bond albedo, we have albedo data at four colors. The study of these relative albedos is really a new topic, and we are not sure what climatological information may be contained therein. We propose to explore the correlation between cloud cover and the ratio of each of the four color albedos to the Bond albedo.
We are requesting funds to support a postdoctoral associate and half an observer. During the first year, we request funds to buy a 16-bit, 512x512 visible light CCD camera system to supplant the one used in earlier observations. The camera system we have in mind is from Apogee Systems (AP-7: $15K including camera, computer and capture board). The AP-7 is stable for the extremely long exposure times necessary for Earthshine observations. BBSO will support the observations with its facilities and IR cameras. Goode, Koonin and Wang will be donating time to the earthshine project. Goode and Wang are faculty members at NJIT, and their salaries are primarily paid by their institutions. Goode is the Director of the Observatory and Wang is the Associate Director. Koonin is Vice-President and Provost at Caltech as well as being a member of the faculty.
We estimate that the observational work would constitute a half-time job. The half-time observer might be half supported for daytime observations, as well. The latter support would come from other grants.
The basic operational plan is to divide the postdoctoral position between two people who would receive the rest of their support from other grants. They would reside and work in Big Bear - working as a team on earthshine. The team would work closely with the half-time observer.
The BBSO earthshine team will spend a minimum of one day every other week with Koonin on the Caltech campus working on various aspects of the project, especially the modeling.