| Recently Published (ApJ 756, 2012): Mini-granulation in the Solar Photosphere |
Read More ... |

Observations of the solar surface granulation with the NST with a broad-band TiO filter
showed a presence of two populations of the solar granulation: regular granules of 600-2000
km extent and mini-granules of less than 600 km extent. The two populations show different
size distribution functions and different preferable location on the solar surface.
A data set of 36 images of solar granulation in a quiet sun area on the solar disk center was
analyzed. The data were obtained with the 1.6~m clear aperture New Solar Telescope (NST)
at Big Bear Solar Observatory (BBSO) and with a broad-band filter centered at the TiO (705.7~nm) spectral
line.
A histogram of normalized intensity image (left)
derived from 648 images of 755x700 pixels each shows that the NST imager is
able to capture a wide dynamical spectra of intensities ranging from 0.4 to
2.5.
A very high spatial resolution of the data (diffraction limit of 77~km and
pixel scale of 0.0375'') augmented by the very high contrast of the observed
granulation (15.5±0.6%) allowed us to detect for the first time a distinct
population of mini-granules. On spatial scales below 600~km, mini-granules
dominate the granulation field. Their size is distributed log-normally with no
predominant scale. Conversely, regular (large) granules display a Gaussian
(normal) size distribution with a mode of 1100~km.
Mini-granules contribute
significantly to the total granule area. They are predominantly confined to the
wide dark lanes between regular granules and often form chains and clusters,
see the movie (link) where mini-granules are outlined by yellow contours.
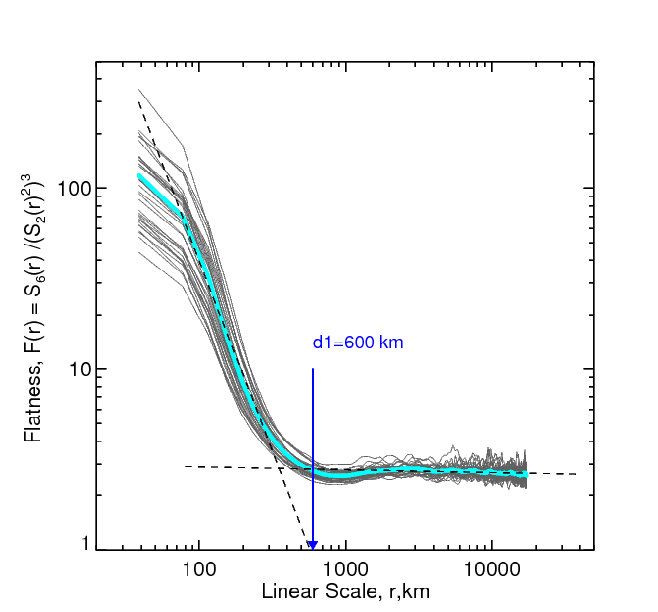
A multi-fractality test reveals that intensity structures smaller that 600~km
represent a multi-fractal, whereas larger features show no multi-fractality and
can be considered as a Gaussian random field. The origin, properties and role of
the newly discovered population of mini-granules in the solar magneto-convection
are yet to be explored.
 |
 |
 |
| Figure 1: A histogram of normalized intensity derived from 648 images of 755x700 pixels each. The NST imager is
able to capture a wide dynamical spectra of intensities ranging from 0.4 to 2.5. (click picture to zoom in) |
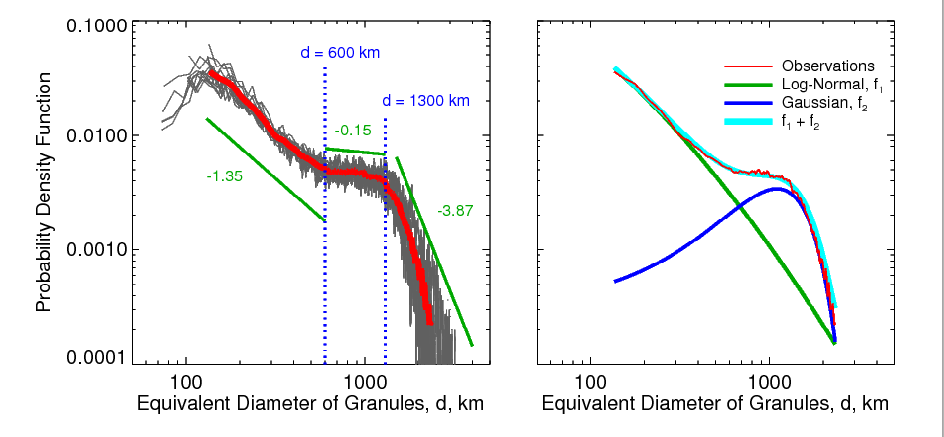
Figure 2: Probability density functions (PDFs) of the granule equivalent diameter derived from 15 various detection runs (gray lines). They are overplotted with their
average (thick red line). The green line segments and numbers show the best
linear fit and the average slope within the corresponding scale range. The most right frame is
decomposition of the observed averaged PDF into two components: a
log-normal approximation, (f1) and a Gaussian approximation
(f2). Their sum (f1+f2) fits the observed data very well. |
Figure 3: Flatness functions calculated from 36 independent granulation images (gray) and their average (turquoise) are shown in the figure to the left. The dashed
segments show the best linear fits to the data points. The blue arrow divides
the multi-fractality range of mini-granules (where the flatness function varies
as a power law) from the Gaussian range of regular granules (where the flatness
function is independent from scales). |
We believe that there exists a smooth transition from the normal granulation to
mini-granulation. The association between the mini-granulation and magnetic and
velocity fields, as well as efforts to detect mini-granulation in numerical
simulations of solar magneto-convection are subjects for future research. As
for now, it is evident that the complex picture of solar near-surface
magneto-convection became even more complex.
| Recent Published: Super-diffusivity in the Quiet Sun Photosphere |
Read More ... |
 |
| Figure 1: Example of bright points detection |
Diffusion of magnetic elements on the solar surface was explored via tracking of photospheric bright
points (BPs) visible in broad-band images. The data sets for a quiet sun area (QS), coronal hole (CH)
and active region's plage area (ARP) were obtained with the NDT with a TiO broad-band filter. All data
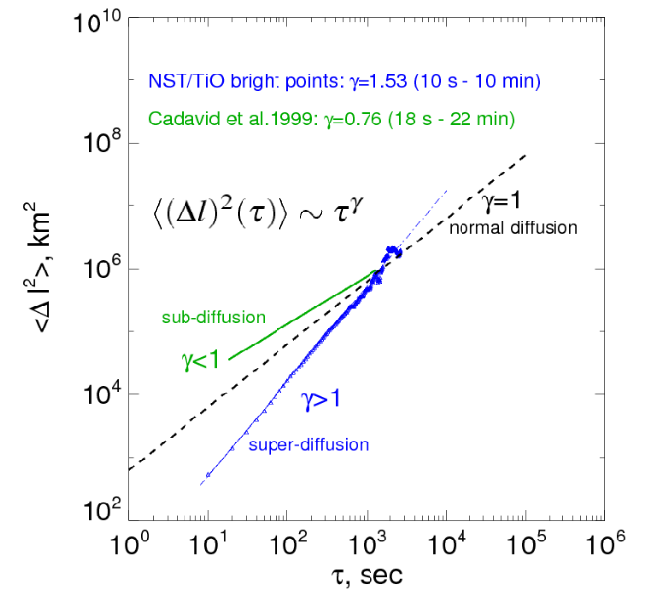
sets showed a regime of super-diffusivity in a good agreement with the diffusivity from simulated data
provided by R. Stein. BPs were automatically detected (an example of detection is shown in Fifure 1).
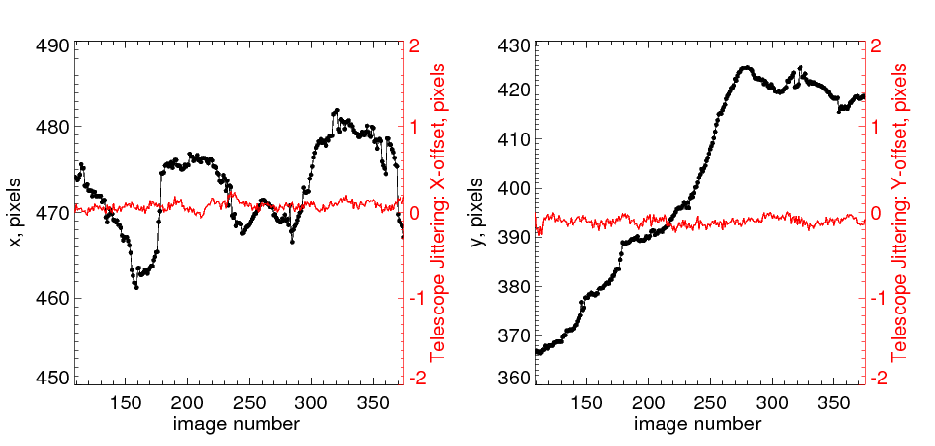
Examples of BPs trajectories are shown in Figure 2. Resudual juttering of the telecsope was very
small as compared to measured displacements of BPs, see Figure 3.
 |
 |
 |
| Figure 2: Example of trajectories of bright poins (click picture to zoom in) |
Figure 3: x- and y-coordinates of a BP overplotted with co-temporal variations of the offset
between two consecutive images (red lines, right axes) |
Figure 4: Trajectories (red) of all BPs detected from the QS data set and persisted longer than 3
time steps (30 sec). Background is the first image of the data set. |
By tracking the BPs we were able to measure their displacements as a function of time.
Displacements were calculated for time intervals between a given moment and the moment when a PB was
first detected. We then calculated the average (over all BPs) displacement for each time interval to obtain
the average squared displacement as a function of time.
 |
 |
 |
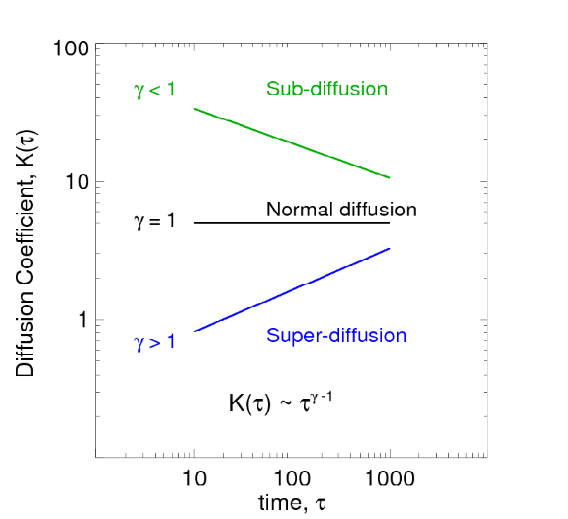
| Figure 5: Qualitative illustration of different regimes of diffusivity. In the case of normal
diffusion, the power index gamma is equal to unity (dashed line).
For sub-diffusivity gamma is less than unity (green; - example: results of Cadavid et al. 1999).
For super-diffusivity, gamma is larger than unity (blue, this study).
|
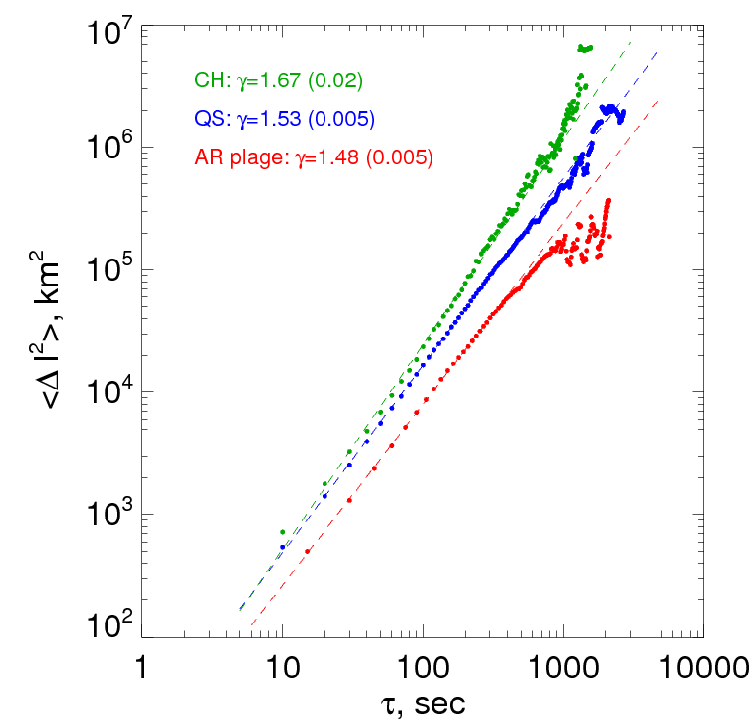
Figure 6: Displacement spectra determined for the CH data (green), QS area (blue), and ARP area (red).
The super-diffusion regime is persistent in all three magnetic areas. The ARP spectrum shows the shallowest
slope and smallest displacements, indicating the lowest level of turbulent diffusion. The CH data show the
steepest spectrum and largest displacements.
|
Figure 7: Displacement spectra for the QS area calculated as a displacements from the start point
(Drift) and as a separation between pairs of BPs (pair separation). The displacement spectrum (drift)
obtained from simulated data is shown in green.
|
 |
 |
 |
| Figure 8: A sketch illustrating how the turbulent diffusion coefficient varies as a function of
time scale for three different regimes of diffusivity. A dependence of the coefficient from the spatial scale
is similar.
|
Figure 9: Turbulent diffusion coefficient plotted as a function of time scale.
|
Figure 10: Turbulent diffusion coefficient plotted as a function of spatial scale. The present study
(solid lines) shows that as the temporal and spatial scales decrease, the diffusion coefficient decreases, too.
|
Modern models of the small-scale turbulent dynamo in the photosphere (Boldyrev
and Cattaneo 2004; Vogler and Schussler 2007; Pietarila Graham et al.
2009) utilize the collisional value of magnetic diffusivity (0.01 - 10
kilometers squared per second) based on the electric conductivity in the photosphere. At the
same time, utilizing the turbulent magnetic diffusivity would be more justified
physically, as long as the turbulent diffusivity determines the minimum scale
for magnetic elements. The measured so far value of turbulent magnetic
diffusivity (70-350 kilometers squared per second) and been interpreted as a scale-independent
parameter, leave a very slim chance to successfully model the small-scale
turbulent dynamo in the photosphere. Thus, in the case of very high diffusivity
on very small scales (sub-diffusivity), chances for tiny magnetic field
concentrations to resist the spreading action of turbulent flows are small, so
that the dynamo is restrained. A super-diffusion regime on very small scales is
very favorable for pictures assuming the turbulent dynamo action since it
assumes decreasing diffusivity with decreasing scales.













