Statistical Distributions of Speeds of Coronal Mass Ejections

Vasyl Yurchyshyn, Seiji Yashiro, Valentyna Abramenko, Haimin Wang and Nat Gopalswamy

Abstract. We analyzed the distribution of speeds of 4315 CMEs published in The CME Catalog at the CDAW data center. We found that the speed distributions for accelerating and decelerating events are nearly identical (X2=0.0033) and to a good approximation they can be fitted with a single log-normal distribution. This finding implies that, statistically, there is no physical distinction between the accelerating and the decelerating events.The log-normal distribution of CME speeds suggests that the same driving mechanism of a non-linear nature is acting in both slow and fast dynamical types of CMEs.

Click here for a MS Power Point version of the poster presented at SHINE 2004 or here for a PDF manuscript of the corresponding ApJ paper.
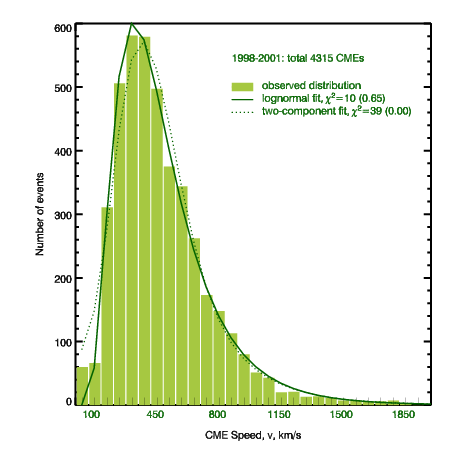
CME Speed Distribution

Figure 1. Linear-linear representation of the distribution of the number of CMEs, N, versus their speeds, v, determined from the linear fit to LASCO data.

The skewed form of the distribution suggests that it may be modeled either with a single log-normal distribution or a sum of a log-normal and a Gaussian distributions(two component fit). It is said that if a random variable (in our case the speed of a CME) is log-normally distributed then its natural logarithm is normally distributed. The log-normal fit (solid line) captures the intensity of the observed distribution in all speed ranges. The two-component fit (dashed line) fails to accurately represent the data in the low speed range below 200 km/s. Because the single log-normal fit better models the data (X2=10 versus X2=39 for the two-component fit), while requiring less free parameters, we conclude that the speeds of CMEs are distributed log-normally (Figure 2, log-linear plot of N vs v).
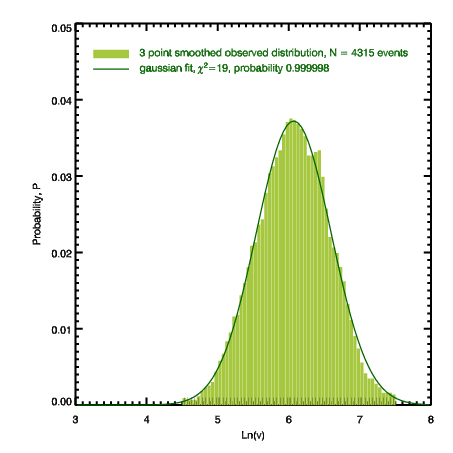
Log-Linear plot of CME Speeds

Figure 2. Log-linear representation of the distribution of the number of CMEs, N, versus their speeds, v, determined from the linear fit to LASCO data.

We separated all events into two groups based on the sign of the acceleration (determined from the 2nd order fit, Figures 3 and 4). We found that the normal approximations for distribution of ln(v) determined for accelerating and decelerating events are the same (X2=0.0033). The largest difference between them is that the accelerating CMEs, as a group, are slightly slower then the decelerating ones. This finding implies  that, statistically, there is no physical distinction between the accelerating and the decelerating events. It also suggests that in the case there do exist two types of CMEs, the physical distinction between them can not be easily revealed.

Conclusion. The single log-normal distribution suggests: i) that the same driving mechanism is acting in both dynamical types of CMEs;  ii) that the speed distribution is a product of a a number of independent random variables, which may arise through the fragmentation process or a multiplicative random cascade; iii) the presence of nonlinear interactions and multiplicative processes in a system of many magnetic flux loops. The driving mechanism is then a multiple reconnection process in a fragmented magnetic field?
Log-Linear Plot for Accelerating Events
Figure 3. Log-linear representation of the distribution of the number of accelerating CMEs, N, versus their speeds, v, determined from the linear fit to LASCO data.
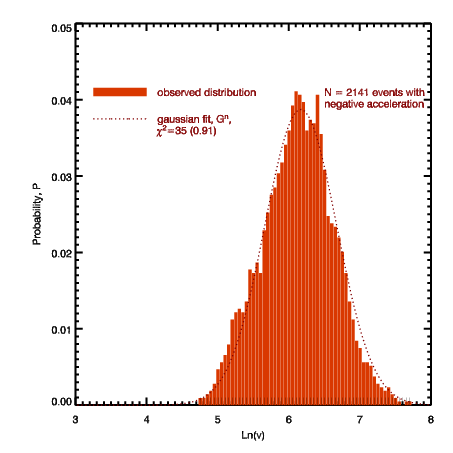Log-Linear Plot for Decelerating Events
Figure 4. Log-linear representation of the distribution of the number of decelerating CMEs, N, versus their speeds, v, determined from the linear fit to LASCO data.
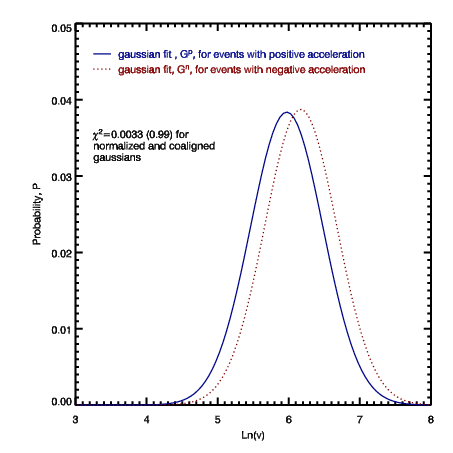Lognormal Fits
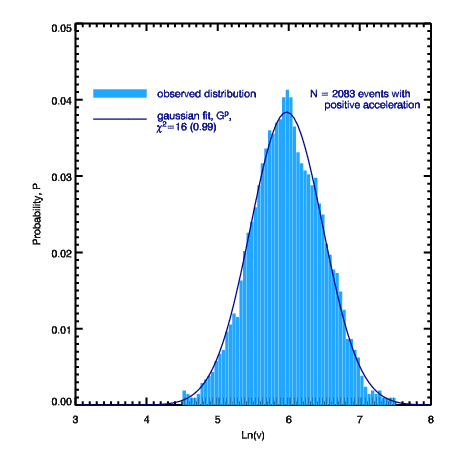
Figure 5. Gaussina fits to N vs ln(v) for accelerating (solid) and decelerating (dotted) events.

(C) Vasyl Yurchyshyn, BBSO/NJIT, November 2, 2004